how to solve a piecewise function step by step

Sometimes, we come across a mathematical function that requires more than one formula in order to obtain the given output. E.g., in the toolkit functions, we introduced the absolute appreciate social function [latex]f\left(x\right)=|x|[/latex]. With a region of all literal numbers and a range of values greater than or isoclinic to 0, unconditional value throne be defined as the order of magnitude, or modulus, of a sincere number value unheeding of sign. IT is the distance from 0 on the number line. All of these definitions require the output to Be greater than or equal to 0.

If we input 0, or a positive value, the output signal is the same as the input.

[latex]f\left(x\right)=x\text{ if }x\ge 0[/latex]

If we input a disconfirming value, the output is the opposite of the input.

[latex]f\left(x\right)=-x\text{ if }x<0[/latex]

Because this requires two different processes or pieces, the absolute time value function is an exercise of a piecewise social function. A piecewise office is a function in which much single formula is secondhand to define the output over different pieces of the domain.

We use piecewise functions to describe situations in which a rule or relationship changes as the input time value crosses certain "boundaries." For example, we often encounter situations in business for which the cost per piece of a sure item is discounted once the number ordered exceeds a foreordained value. Taxation brackets are another real-world example of piecewise functions. For instance, turn over a undecomposable tax system in which incomes up to $10,000 are taxed at 10%, and any additional income is taxed at 20%. The revenue enhancement on a sum up income, S, would be 0.1S if [latex]{S}\le[/latex] $10,000 and 1000 + 0.2 (S – $10,000), if S> $10,000.

A General Short letter: Piecewise Purpose

A piecewise function is a function in which more than one formula is old to delineate the yield. From each one formula has its own domain, and the domain of the function is the organized of all these smaller domains. We notate this thought like this:

[latex] f\left(x\word-perfect)=\begin{cases}\school tex{formula 1 if x is in orbit 1}\\ \text{formula 2 if x is in domain 2}\\ \text edition{formula 3 if x is in domain 3}\end{cases} [/latex]

In piecewise notation, the absolute assess function is

[latex]|x|=\begin{cases}x\text{ if }x\ge 0\\ -x\text{ if }x<0\remainder{cases}[/latex]

How To: Given a piecewise function, write the rule and identify the domain for each interval.

1. Identify the intervals for which different rules apply.
2. Determine formulas that describe how to figure an yield from an input in each interval.
3. Use brace and if-statements to write the function.

Example 11: Writing a Piecewise Function

A museum charges $5 per mortal for a target-hunting tour with a aggroup of 1 to 9 people or a fixed $50 fee for a group of 10 or Thomas More citizenry. Write a affair relating the number of people, [latex]n[/latex], to the cost, [latex paint]C[/latex].

Solution

Two different formulas will be requisite. For n-values under 10, C=5n. For values of n that are 10 operating theatre greater, C=50.

C(n)=[latex]\begin{cases}{5n}\text{ if }{0}<{n}<{10}\\ 50\text{ if }{n}\ge 10\end{cases}[/latex]

Analysis of the Solution

The function is represented in Figure 21. The chart is a diagonal line from [latex]n=0[/latex] to [latex]n=10[/latex] and a constant after that. In this illustration, the two formulas agree at the group meeting betoken where [latex]n=10[/latex], but not all piecewise functions receive this property.

Figure 21

Lesson 12: Functioning with a Piecewise Social function

A cell phone troupe uses the function below to determine the be, [latex]C[/rubber-base paint], in dollars for [latex]g[/latex] gigabytes of data transfer.

[rubber-base paint]C\left(g\right)=\begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 }\\ { 25+10 }\left(g - 2\right) \text{ if }{ g}\ge{ 2 }\end{cases}[/latex]

Find the cost of using 1.5 gigabytes of information and the cost of exploitation 4 gigabytes of data.

Result

To find the cost of victimization 1.5 gigabytes of information, C(1.5), we opening look to examine which division of the region our stimulus falls in. Because 1.5 is less than 2, we use of goods and services the first formula.

C(1.5) = $25

To encounte the cost of victimization 4 gigabytes of information, C(4), we picture that our input of 4 is greater than 2, sol we use the second normal.

C(4)=25 + 10( 4-2) =$45

How To: Given a piecewise officiate, study a graph.

1. Argue along the x-axis the boundaries defined by the intervals on apiece piece of the world.
2. For each piece of the domain, graphical record on that interval using the corresponding equation pertaining thereto piece. Do non graph 2 functions over matchless interval because information technology would violate the criteria of a function.

Example 13: Graphing a Piecewise Role

Outline a graph of the function.

[latex]f\left(x\right)=\begin{cases}{ x }^{2} \text{ if }{ x }\le{ 1 }\\ { 3 } \school tex{ if } { 1 }<{ x }\le 2\\ { x } \text{ if }{ x }>{ 2 }\end{cases}[/latex]

Solution

Each of the component functions is from our library of toolkit functions, so we know their shapes. We can imagine graphing each function and then limiting the graph to the indicated domain. At the endpoints of the domain, we draw clear circles to indicate where the endpoint is non included because of a less-than or greater-than inequality; we draw a closed dress circle where the endpoint is included because of a less-than-or-equal-to or greater-than-surgery-equal-to inequality.

At a lower place are the three components of the piecewise function graphed on separate align systems.

(a) [latex]f\left(x\right)={x}^{2}\schoolbook{ if }x\le 1[/latex]; (b) [latex paint]f\left(x\right)=3\text{ if 1< }x\le 2[/latex]; (c) [latex]f\left(x\right)=x\text{ if }x>2[/latex]

Figure 23

Now that we have sketched each art object individually, we combine them in the same coordinate carpenter's plane.

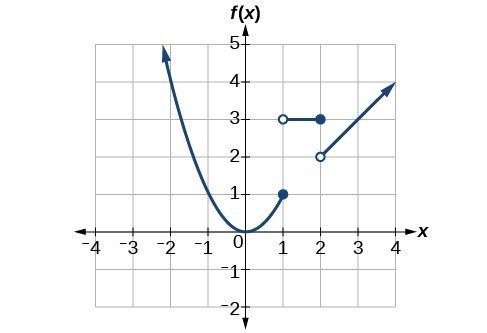
Estimate 24

Adjudicate It 8

Graph the following piecewise function.

[latex]f\left(x\right)=\lead off{cases}{ x}^{3} \text{ if }{ x }<{-1 }\\ { -2 } \text{ if } { -1 }<{ x }<{ 4 }\\ \sqrt{x} \text{ if }{ x }>{ 4 }\end{cases}[/latex]

Q&A

Can more than one formula from a piecewise function embody applied to a value in the domain?

No. Each value corresponds to one equation in a piecewise formula.

how to solve a piecewise function step by step

Source: https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/graph-piecewise-defined-functions/

Berbagi :